The world of mathematics is advanced, but not completely impossible! This article explores the fundamentals of the triangle law of vector addition, making it an accessible and engaging topic for students.
What Is Triangle Law Of Vector Addition?
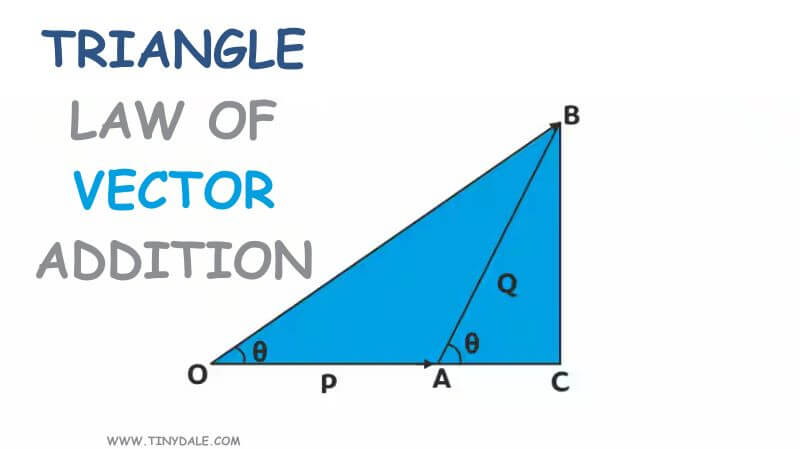
The Triangle Law of Vector Addition states that when two vectors are represented as sides of a triangle, the resultant vector, connecting the origin to the third side, is the vector sum of the two original vectors.
This law illustrates vector addition geometrically, showing that the order in which vectors are added does not affect the result. It is a fundamental concept in physics and engineering, essential for understanding and analyzing forces, velocities, and other vector quantities. Source
What Is Vector Addition?
Vector addition is a mathematical operation that combines multiple vectors to determine their resultant vector. Additionally, vectors are quantities with magnitude and direction, such as force, velocity, or displacement.
To add vectors, you align them tail-to-head and then connect the tail of the first vector to the head of the next, forming a series of connected vectors. The resultant vector connects the initial tail to the final head in this sequence.
Mathematically, vector addition involves summing the individual components of the vectors, considering both magnitude and direction. This concept is crucial in physics, engineering, and various fields to analyze forces, motion, and various vector-related phenomena. Source
Formula For Triangle Law Of Vector Addition
The Triangle Law of Vector Addition does not have a specific formula, as it is a geometric method for adding vectors. Instead, it is typically represented visually as follows:
- Draw two vectors, A and B, with their tails at the same point.
- Complete the triangle by drawing a line from the tail of vector A to the head of vector B. This line represents the resultant vector, R.
Mathematically, you can express this as:
R = A + B
Where:
- R is the resultant vector.
- A is the first vector.
- B is the second vector.
To find the magnitude and direction of R, you can use trigonometric methods or break down the vectors into their components and add them separately.
Derivation Of Triangle Law Of Vector Addition
The Triangle Law of Vector Addition can be derived using vector components and basic geometry. Let’s consider two vectors A and B, and we want to find their resultant vector R.
Begin by expressing vectors A and B in terms of their components along two perpendicular axes, typically the x and y axes. For example:
A = A_xi + A_yj
- B = B_xi + B_yj
Now, add the corresponding components of A and B:
R_x = A_x + B_x
- R_y = A_y + B_y
- Combine these components to find the resultant vector R:
R = R_xi + R_yj
This derivation is based on the principle that adding vector components along each axis independently is equivalent to adding the vectors graphically using the Triangle Law. It’s a fundamental application of vector algebra and geometry, providing a mathematical way to calculate the resultant vector from the individual vectors’ components.
FAQs
Q1: What is the Triangle Law of Vector Addition?
A1: The Triangle Law of Vector Addition states that if two vectors are represented by two sides of a triangle in both direction and magnitude, then the third side of the triangle represents the resultant vector both in magnitude and direction.
Q2: Can you explain the Triangle Law with an example?
A2: Certainly! Imagine two vectors A and B represented by two sides of a triangle.
Q3: Does the order of vectors matter in the Triangle Law?
A3: No, the order of vectors does not matter in the Triangle Law of Vector Addition. You can start with any vector and draw the other vectors in the order given.
Q4: Can the Triangle Law be applied to more than two vectors?
A4: Yes, the Triangle Law can be extended to more than two vectors. If you have multiple vectors that need to be added, you can apply the Triangle Law iteratively.
Q5: Is the Triangle Law applicable only to specific types of vectors?
A5: No, it is applicable to all types of vectors, including displacement vectors, force vectors, velocity vectors, and so on.
Summary!
In conclusion, mastering the Triangle Law of Vector Addition is a crucial step in understanding vector mathematics. Empowering students with this knowledge equips them to tackle complex problems and opens the door to a world of applications in physics, engineering, and more.
Also Read: 80 Amazing Aunt And Nephew/Niece Quotes!
Tinydale is on YouTube, Click here to subscribe for the latest videos and updates.
Follow Us: Facebook | Instagram | Twitter | Youtube | Pinterest